Note
Click here to download the full example code
Spatial Transformer Networks Tutorial¶
Author: Ghassen HAMROUNI

In this tutorial, you will learn how to augment your network using a visual attention mechanism called spatial transformer networks. You can read more about the spatial transformer networks in the DeepMind paper
Spatial transformer networks are a generalization of differentiable attention to any spatial transformation. Spatial transformer networks (STN for short) allow a neural network to learn how to perform spatial transformations on the input image in order to enhance the geometric invariance of the model. For example, it can crop a region of interest, scale and correct the orientation of an image. It can be a useful mechanism because CNNs are not invariant to rotation and scale and more general affine transformations.
One of the best things about STN is the ability to simply plug it into any existing CNN with very little modification.
# License: BSD
# Author: Ghassen Hamrouni
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy as np
plt.ion() # interactive mode
Loading the data¶
In this post we experiment with the classic MNIST dataset. Using a standard convolutional network augmented with a spatial transformer network.
from six.moves import urllib
opener = urllib.request.build_opener()
opener.addheaders = [('User-agent', 'Mozilla/5.0')]
urllib.request.install_opener(opener)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Training dataset
train_loader = torch.utils.data.DataLoader(
datasets.MNIST(root='.', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])), batch_size=64, shuffle=True, num_workers=4)
# Test dataset
test_loader = torch.utils.data.DataLoader(
datasets.MNIST(root='.', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])), batch_size=64, shuffle=True, num_workers=4)
Out:
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to ./MNIST/raw/train-images-idx3-ubyte.gz
Extracting ./MNIST/raw/train-images-idx3-ubyte.gz to ./MNIST/raw
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to ./MNIST/raw/train-labels-idx1-ubyte.gz
Extracting ./MNIST/raw/train-labels-idx1-ubyte.gz to ./MNIST/raw
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to ./MNIST/raw/t10k-images-idx3-ubyte.gz
Extracting ./MNIST/raw/t10k-images-idx3-ubyte.gz to ./MNIST/raw
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to ./MNIST/raw/t10k-labels-idx1-ubyte.gz
Extracting ./MNIST/raw/t10k-labels-idx1-ubyte.gz to ./MNIST/raw
Depicting spatial transformer networks¶
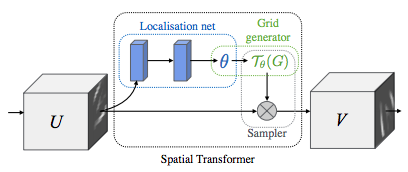
Spatial transformer networks boils down to three main components :
- The localization network is a regular CNN which regresses the transformation parameters. The transformation is never learned explicitly from this dataset, instead the network learns automatically the spatial transformations that enhances the global accuracy.
- The grid generator generates a grid of coordinates in the input image corresponding to each pixel from the output image.
- The sampler uses the parameters of the transformation and applies it to the input image.
Note
We need the latest version of PyTorch that contains affine_grid and grid_sample modules.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
# Spatial transformer localization-network
self.localization = nn.Sequential(
nn.Conv2d(1, 8, kernel_size=7),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True),
nn.Conv2d(8, 10, kernel_size=5),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True)
)
# Regressor for the 3 * 2 affine matrix
self.fc_loc = nn.Sequential(
nn.Linear(10 * 3 * 3, 32),
nn.ReLU(True),
nn.Linear(32, 3 * 2)
)
# Initialize the weights/bias with identity transformation
self.fc_loc[2].weight.data.zero_()
self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))
# Spatial transformer network forward function
def stn(self, x):
xs = self.localization(x)
xs = xs.view(-1, 10 * 3 * 3)
theta = self.fc_loc(xs)
theta = theta.view(-1, 2, 3)
grid = F.affine_grid(theta, x.size())
x = F.grid_sample(x, grid)
return x
def forward(self, x):
# transform the input
x = self.stn(x)
# Perform the usual forward pass
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x, dim=1)
model = Net().to(device)
Training the model¶
Now, let’s use the SGD algorithm to train the model. The network is learning the classification task in a supervised way. In the same time the model is learning STN automatically in an end-to-end fashion.
optimizer = optim.SGD(model.parameters(), lr=0.01)
def train(epoch):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % 500 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
#
# A simple test procedure to measure the STN performances on MNIST.
#
def test():
with torch.no_grad():
model.eval()
test_loss = 0
correct = 0
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
# sum up batch loss
test_loss += F.nll_loss(output, target, size_average=False).item()
# get the index of the max log-probability
pred = output.max(1, keepdim=True)[1]
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'
.format(test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
Visualizing the STN results¶
Now, we will inspect the results of our learned visual attention mechanism.
We define a small helper function in order to visualize the transformations while training.
def convert_image_np(inp):
"""Convert a Tensor to numpy image."""
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
return inp
# We want to visualize the output of the spatial transformers layer
# after the training, we visualize a batch of input images and
# the corresponding transformed batch using STN.
def visualize_stn():
with torch.no_grad():
# Get a batch of training data
data = next(iter(test_loader))[0].to(device)
input_tensor = data.cpu()
transformed_input_tensor = model.stn(data).cpu()
in_grid = convert_image_np(
torchvision.utils.make_grid(input_tensor))
out_grid = convert_image_np(
torchvision.utils.make_grid(transformed_input_tensor))
# Plot the results side-by-side
f, axarr = plt.subplots(1, 2)
axarr[0].imshow(in_grid)
axarr[0].set_title('Dataset Images')
axarr[1].imshow(out_grid)
axarr[1].set_title('Transformed Images')
for epoch in range(1, 20 + 1):
train(epoch)
test()
# Visualize the STN transformation on some input batch
visualize_stn()
plt.ioff()
plt.show()

Out:
Train Epoch: 1 [0/60000 (0%)] Loss: 2.368588
Train Epoch: 1 [32000/60000 (53%)] Loss: 0.916856
Test set: Average loss: 0.4112, Accuracy: 8697/10000 (87%)
Train Epoch: 2 [0/60000 (0%)] Loss: 0.908913
Train Epoch: 2 [32000/60000 (53%)] Loss: 0.345142
Test set: Average loss: 0.1291, Accuracy: 9593/10000 (96%)
Train Epoch: 3 [0/60000 (0%)] Loss: 0.250927
Train Epoch: 3 [32000/60000 (53%)] Loss: 0.421475
Test set: Average loss: 0.1086, Accuracy: 9668/10000 (97%)
Train Epoch: 4 [0/60000 (0%)] Loss: 0.350522
Train Epoch: 4 [32000/60000 (53%)] Loss: 0.257925
Test set: Average loss: 0.2147, Accuracy: 9354/10000 (94%)
Train Epoch: 5 [0/60000 (0%)] Loss: 0.305506
Train Epoch: 5 [32000/60000 (53%)] Loss: 0.082600
Test set: Average loss: 0.0722, Accuracy: 9768/10000 (98%)
Train Epoch: 6 [0/60000 (0%)] Loss: 0.212339
Train Epoch: 6 [32000/60000 (53%)] Loss: 0.183269
Test set: Average loss: 0.0848, Accuracy: 9741/10000 (97%)
Train Epoch: 7 [0/60000 (0%)] Loss: 0.096175
Train Epoch: 7 [32000/60000 (53%)] Loss: 0.140066
Test set: Average loss: 0.0562, Accuracy: 9827/10000 (98%)
Train Epoch: 8 [0/60000 (0%)] Loss: 0.126675
Train Epoch: 8 [32000/60000 (53%)] Loss: 0.115889
Test set: Average loss: 0.0520, Accuracy: 9836/10000 (98%)
Train Epoch: 9 [0/60000 (0%)] Loss: 0.131406
Train Epoch: 9 [32000/60000 (53%)] Loss: 0.263442
Test set: Average loss: 0.0458, Accuracy: 9866/10000 (99%)
Train Epoch: 10 [0/60000 (0%)] Loss: 0.093719
Train Epoch: 10 [32000/60000 (53%)] Loss: 0.089051
Test set: Average loss: 0.0555, Accuracy: 9830/10000 (98%)
Train Epoch: 11 [0/60000 (0%)] Loss: 0.225552
Train Epoch: 11 [32000/60000 (53%)] Loss: 0.092615
Test set: Average loss: 0.0527, Accuracy: 9840/10000 (98%)
Train Epoch: 12 [0/60000 (0%)] Loss: 0.420041
Train Epoch: 12 [32000/60000 (53%)] Loss: 0.050414
Test set: Average loss: 0.0470, Accuracy: 9863/10000 (99%)
Train Epoch: 13 [0/60000 (0%)] Loss: 0.097507
Train Epoch: 13 [32000/60000 (53%)] Loss: 0.069199
Test set: Average loss: 0.0468, Accuracy: 9855/10000 (99%)
Train Epoch: 14 [0/60000 (0%)] Loss: 0.207414
Train Epoch: 14 [32000/60000 (53%)] Loss: 0.027101
Test set: Average loss: 0.0422, Accuracy: 9871/10000 (99%)
Train Epoch: 15 [0/60000 (0%)] Loss: 0.091398
Train Epoch: 15 [32000/60000 (53%)] Loss: 0.211614
Test set: Average loss: 0.0369, Accuracy: 9887/10000 (99%)
Train Epoch: 16 [0/60000 (0%)] Loss: 0.035318
Train Epoch: 16 [32000/60000 (53%)] Loss: 0.092014
Test set: Average loss: 0.0369, Accuracy: 9890/10000 (99%)
Train Epoch: 17 [0/60000 (0%)] Loss: 0.055495
Train Epoch: 17 [32000/60000 (53%)] Loss: 0.119085
Test set: Average loss: 0.0412, Accuracy: 9870/10000 (99%)
Train Epoch: 18 [0/60000 (0%)] Loss: 0.028833
Train Epoch: 18 [32000/60000 (53%)] Loss: 0.044220
Test set: Average loss: 0.0388, Accuracy: 9889/10000 (99%)
Train Epoch: 19 [0/60000 (0%)] Loss: 0.074087
Train Epoch: 19 [32000/60000 (53%)] Loss: 0.046246
Test set: Average loss: 0.0690, Accuracy: 9816/10000 (98%)
Train Epoch: 20 [0/60000 (0%)] Loss: 0.154425
Train Epoch: 20 [32000/60000 (53%)] Loss: 0.059043
Test set: Average loss: 0.0380, Accuracy: 9894/10000 (99%)
Total running time of the script: ( 2 minutes 45.248 seconds)



