Language Modeling with nn.Transformer and TorchText

This is a tutorial on training a sequence-to-sequence model that uses the nn.Transformer module.

The PyTorch 1.2 release includes a standard transformer module based on the paper Attention is All You Need. Compared to Recurrent Neural Networks (RNNs), the transformer model has proven to be superior in quality for many sequence-to-sequence tasks while being more parallelizable. The nn.Transformer module relies entirely on an attention mechanism (implemented as nn.MultiheadAttention) to draw global dependencies between input and output. The nn.Transformer module is highly modularized such that a single component (e.g., nn.TransformerEncoder) can be easily adapted/composed.

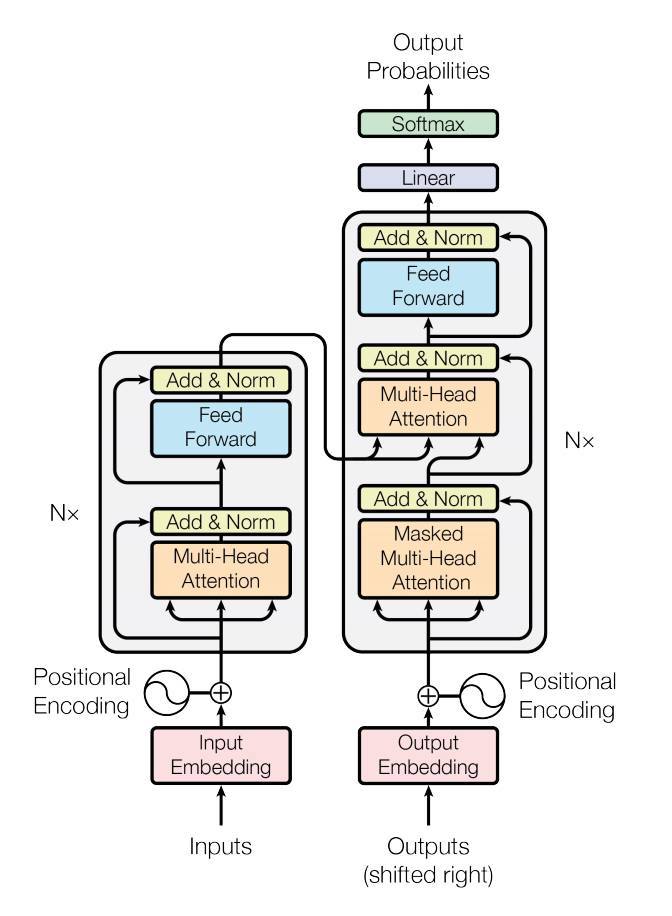
Define the model

In this tutorial, we train a nn.TransformerEncoder model on a language modeling task. The language modeling task is to assign a probability for the likelihood of a given word (or a sequence of words) to follow a sequence of words. A sequence of tokens are passed to the embedding layer first, followed by a positional encoding layer to account for the order of the word (see the next paragraph for more details). The nn.TransformerEncoder consists of multiple layers of nn.TransformerEncoderLayer. Along with the input sequence, a square attention mask is required because the self-attention layers in nn.TransformerEncoder are only allowed to attend the earlier positions in the sequence. For the language modeling task, any tokens on the future positions should be masked. To produce a probability distribution over output words, the output of the nn.TransformerEncoder model is passed through a linear layer followed by a log-softmax function.

import math
from typing import Tuple

import torch
from torch import nn, Tensor
import torch.nn.functional as F
from torch.nn import TransformerEncoder, TransformerEncoderLayer
from torch.utils.data import dataset

class TransformerModel(nn.Module):

    def __init__(self, ntoken: int, d_model: int, nhead: int, d_hid: int,
                 nlayers: int, dropout: float = 0.5):
        super().__init__()
        self.model_type = 'Transformer'
        self.pos_encoder = PositionalEncoding(d_model, dropout)
        encoder_layers = TransformerEncoderLayer(d_model, nhead, d_hid, dropout)
        self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)
        self.encoder = nn.Embedding(ntoken, d_model)
        self.d_model = d_model
        self.decoder = nn.Linear(d_model, ntoken)

        self.init_weights()

    def init_weights(self) -> None:
        initrange = 0.1
        self.encoder.weight.data.uniform_(-initrange, initrange)
        self.decoder.bias.data.zero_()
        self.decoder.weight.data.uniform_(-initrange, initrange)

    def forward(self, src: Tensor, src_mask: Tensor) -> Tensor:
        """
        Args:
            src: Tensor, shape [seq_len, batch_size]
            src_mask: Tensor, shape [seq_len, seq_len]

        Returns:
            output Tensor of shape [seq_len, batch_size, ntoken]
        """
        src = self.encoder(src) * math.sqrt(self.d_model)
        src = self.pos_encoder(src)
        output = self.transformer_encoder(src, src_mask)
        output = self.decoder(output)
        return output


def generate_square_subsequent_mask(sz: int) -> Tensor:
    """Generates an upper-triangular matrix of -inf, with zeros on diag."""
    return torch.triu(torch.ones(sz, sz) * float('-inf'), diagonal=1)

PositionalEncoding module injects some information about the relative or absolute position of the tokens in the sequence. The positional encodings have the same dimension as the embeddings so that the two can be summed. Here, we use sine and cosine functions of different frequencies.

class PositionalEncoding(nn.Module):

    def __init__(self, d_model: int, dropout: float = 0.1, max_len: int = 5000):
        super().__init__()
        self.dropout = nn.Dropout(p=dropout)

        position = torch.arange(max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))
        pe = torch.zeros(max_len, 1, d_model)
        pe[:, 0, 0::2] = torch.sin(position * div_term)
        pe[:, 0, 1::2] = torch.cos(position * div_term)
        self.register_buffer('pe', pe)

    def forward(self, x: Tensor) -> Tensor:
        """
        Args:
            x: Tensor, shape [seq_len, batch_size, embedding_dim]
        """
        x = x + self.pe[:x.size(0)]
        return self.dropout(x)

Load and batch data

This tutorial uses torchtext to generate Wikitext-2 dataset. To access torchtext datasets, please install torchdata following instructions at https://github.com/pytorch/data.

The vocab object is built based on the train dataset and is used to numericalize tokens into tensors. Wikitext-2 represents rare tokens as <unk>.

Given a 1-D vector of sequential data, batchify() arranges the data into batch_size columns. If the data does not divide evenly into batch_size columns, then the data is trimmed to fit. For instance, with the alphabet as the data (total length of 26) and batch_size=4, we would divide the alphabet into 4 sequences of length 6:

\[\begin{bmatrix} \text{A} & \text{B} & \text{C} & \ldots & \text{X} & \text{Y} & \text{Z} \end{bmatrix} \Rightarrow \begin{bmatrix} \begin{bmatrix}\text{A} \\ \text{B} \\ \text{C} \\ \text{D} \\ \text{E} \\ \text{F}\end{bmatrix} & \begin{bmatrix}\text{G} \\ \text{H} \\ \text{I} \\ \text{J} \\ \text{K} \\ \text{L}\end{bmatrix} & \begin{bmatrix}\text{M} \\ \text{N} \\ \text{O} \\ \text{P} \\ \text{Q} \\ \text{R}\end{bmatrix} & \begin{bmatrix}\text{S} \\ \text{T} \\ \text{U} \\ \text{V} \\ \text{W} \\ \text{X}\end{bmatrix} \end{bmatrix} \]

Batching enables more parallelizable processing. However, batching means that the model treats each column independently; for example, the dependence of G and F can not be learned in the example above.

from torchtext.datasets import WikiText2
from torchtext.data.utils import get_tokenizer
from torchtext.vocab import build_vocab_from_iterator

train_iter = WikiText2(split='train')
tokenizer = get_tokenizer('basic_english')
vocab = build_vocab_from_iterator(map(tokenizer, train_iter), specials=['<unk>'])
vocab.set_default_index(vocab['<unk>'])

def data_process(raw_text_iter: dataset.IterableDataset) -> Tensor:
    """Converts raw text into a flat Tensor."""
    data = [torch.tensor(vocab(tokenizer(item)), dtype=torch.long) for item in raw_text_iter]
    return torch.cat(tuple(filter(lambda t: t.numel() > 0, data)))

# train_iter was "consumed" by the process of building the vocab,
# so we have to create it again
train_iter, val_iter, test_iter = WikiText2()
train_data = data_process(train_iter)
val_data = data_process(val_iter)
test_data = data_process(test_iter)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

def batchify(data: Tensor, bsz: int) -> Tensor:
    """Divides the data into bsz separate sequences, removing extra elements
    that wouldn't cleanly fit.

    Args:
        data: Tensor, shape [N]
        bsz: int, batch size

    Returns:
        Tensor of shape [N // bsz, bsz]
    """
    seq_len = data.size(0) // bsz
    data = data[:seq_len * bsz]
    data = data.view(bsz, seq_len).t().contiguous()
    return data.to(device)

batch_size = 20
eval_batch_size = 10
train_data = batchify(train_data, batch_size)  # shape [seq_len, batch_size]
val_data = batchify(val_data, eval_batch_size)
test_data = batchify(test_data, eval_batch_size)

Functions to generate input and target sequence

get_batch() generates a pair of input-target sequences for the transformer model. It subdivides the source data into chunks of length bptt. For the language modeling task, the model needs the following words as Target. For example, with a bptt value of 2, we’d get the following two Variables for i = 0:

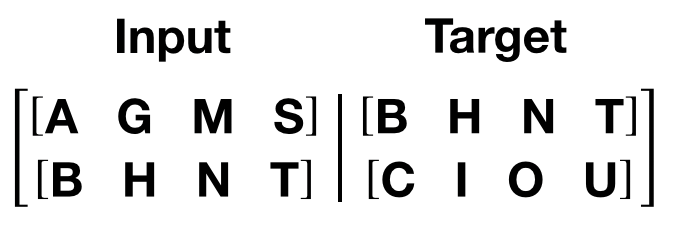
It should be noted that the chunks are along dimension 0, consistent with the S dimension in the Transformer model. The batch dimension N is along dimension 1.

bptt = 35
def get_batch(source: Tensor, i: int) -> Tuple[Tensor, Tensor]:
    """
    Args:
        source: Tensor, shape [full_seq_len, batch_size]
        i: int

    Returns:
        tuple (data, target), where data has shape [seq_len, batch_size] and
        target has shape [seq_len * batch_size]
    """
    seq_len = min(bptt, len(source) - 1 - i)
    data = source[i:i+seq_len]
    target = source[i+1:i+1+seq_len].reshape(-1)
    return data, target

Initiate an instance

The model hyperparameters are defined below. The vocab size is equal to the length of the vocab object.

ntokens = len(vocab)  # size of vocabulary
emsize = 200  # embedding dimension
d_hid = 200  # dimension of the feedforward network model in nn.TransformerEncoder
nlayers = 2  # number of nn.TransformerEncoderLayer in nn.TransformerEncoder
nhead = 2  # number of heads in nn.MultiheadAttention
dropout = 0.2  # dropout probability
model = TransformerModel(ntokens, emsize, nhead, d_hid, nlayers, dropout).to(device)

Run the model

We use CrossEntropyLoss with the SGD (stochastic gradient descent) optimizer. The learning rate is initially set to 5.0 and follows a StepLR schedule. During training, we use nn.utils.clip_grad_norm_ to prevent gradients from exploding.

import copy
import time

criterion = nn.CrossEntropyLoss()
lr = 5.0  # learning rate
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 1.0, gamma=0.95)

def train(model: nn.Module) -> None:
    model.train()  # turn on train mode
    total_loss = 0.
    log_interval = 200
    start_time = time.time()
    src_mask = generate_square_subsequent_mask(bptt).to(device)

    num_batches = len(train_data) // bptt
    for batch, i in enumerate(range(0, train_data.size(0) - 1, bptt)):
        data, targets = get_batch(train_data, i)
        batch_size = data.size(0)
        if batch_size != bptt:  # only on last batch
            src_mask = src_mask[:batch_size, :batch_size]
        output = model(data, src_mask)
        loss = criterion(output.view(-1, ntokens), targets)

        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_norm_(model.parameters(), 0.5)
        optimizer.step()

        total_loss += loss.item()
        if batch % log_interval == 0 and batch > 0:
            lr = scheduler.get_last_lr()[0]
            ms_per_batch = (time.time() - start_time) * 1000 / log_interval
            cur_loss = total_loss / log_interval
            ppl = math.exp(cur_loss)
            print(f'| epoch {epoch:3d} | {batch:5d}/{num_batches:5d} batches | '
                  f'lr {lr:02.2f} | ms/batch {ms_per_batch:5.2f} | '
                  f'loss {cur_loss:5.2f} | ppl {ppl:8.2f}')
            total_loss = 0
            start_time = time.time()

def evaluate(model: nn.Module, eval_data: Tensor) -> float:
    model.eval()  # turn on evaluation mode
    total_loss = 0.
    src_mask = generate_square_subsequent_mask(bptt).to(device)
    with torch.no_grad():
        for i in range(0, eval_data.size(0) - 1, bptt):
            data, targets = get_batch(eval_data, i)
            batch_size = data.size(0)
            if batch_size != bptt:
                src_mask = src_mask[:batch_size, :batch_size]
            output = model(data, src_mask)
            output_flat = output.view(-1, ntokens)
            total_loss += batch_size * criterion(output_flat, targets).item()
    return total_loss / (len(eval_data) - 1)

Loop over epochs. Save the model if the validation loss is the best we’ve seen so far. Adjust the learning rate after each epoch.

best_val_loss = float('inf')
epochs = 3
best_model = None

for epoch in range(1, epochs + 1):
    epoch_start_time = time.time()
    train(model)
    val_loss = evaluate(model, val_data)
    val_ppl = math.exp(val_loss)
    elapsed = time.time() - epoch_start_time
    print('-' * 89)
    print(f'| end of epoch {epoch:3d} | time: {elapsed:5.2f}s | '
          f'valid loss {val_loss:5.2f} | valid ppl {val_ppl:8.2f}')
    print('-' * 89)

    if val_loss < best_val_loss:
        best_val_loss = val_loss
        best_model = copy.deepcopy(model)

    scheduler.step()

Out:

| epoch   1 |   200/ 2928 batches | lr 5.00 | ms/batch 21.70 | loss  8.05 | ppl  3129.79
| epoch   1 |   400/ 2928 batches | lr 5.00 | ms/batch 21.16 | loss  6.84 | ppl   938.76
| epoch   1 |   600/ 2928 batches | lr 5.00 | ms/batch 21.18 | loss  6.42 | ppl   612.54
| epoch   1 |   800/ 2928 batches | lr 5.00 | ms/batch 21.23 | loss  6.28 | ppl   533.89
| epoch   1 |  1000/ 2928 batches | lr 5.00 | ms/batch 21.19 | loss  6.18 | ppl   481.73
| epoch   1 |  1200/ 2928 batches | lr 5.00 | ms/batch 21.16 | loss  6.14 | ppl   466.19
| epoch   1 |  1400/ 2928 batches | lr 5.00 | ms/batch 21.13 | loss  6.10 | ppl   447.26
| epoch   1 |  1600/ 2928 batches | lr 5.00 | ms/batch 21.14 | loss  6.10 | ppl   445.09
| epoch   1 |  1800/ 2928 batches | lr 5.00 | ms/batch 21.15 | loss  6.02 | ppl   409.67
| epoch   1 |  2000/ 2928 batches | lr 5.00 | ms/batch 21.19 | loss  6.00 | ppl   403.92
| epoch   1 |  2200/ 2928 batches | lr 5.00 | ms/batch 21.26 | loss  5.89 | ppl   361.06
| epoch   1 |  2400/ 2928 batches | lr 5.00 | ms/batch 21.18 | loss  5.96 | ppl   389.42
| epoch   1 |  2600/ 2928 batches | lr 5.00 | ms/batch 21.16 | loss  5.94 | ppl   380.71
| epoch   1 |  2800/ 2928 batches | lr 5.00 | ms/batch 21.14 | loss  5.88 | ppl   356.13
-----------------------------------------------------------------------------------------
| end of epoch   1 | time: 64.44s | valid loss  5.83 | valid ppl   338.87
-----------------------------------------------------------------------------------------
| epoch   2 |   200/ 2928 batches | lr 4.75 | ms/batch 21.28 | loss  5.85 | ppl   346.46
| epoch   2 |   400/ 2928 batches | lr 4.75 | ms/batch 21.21 | loss  5.84 | ppl   343.90
| epoch   2 |   600/ 2928 batches | lr 4.75 | ms/batch 21.23 | loss  5.66 | ppl   286.70
| epoch   2 |   800/ 2928 batches | lr 4.75 | ms/batch 21.20 | loss  5.69 | ppl   297.14
| epoch   2 |  1000/ 2928 batches | lr 4.75 | ms/batch 21.25 | loss  5.64 | ppl   282.78
| epoch   2 |  1200/ 2928 batches | lr 4.75 | ms/batch 21.20 | loss  5.67 | ppl   291.41
| epoch   2 |  1400/ 2928 batches | lr 4.75 | ms/batch 21.20 | loss  5.68 | ppl   293.84
| epoch   2 |  1600/ 2928 batches | lr 4.75 | ms/batch 21.21 | loss  5.71 | ppl   300.49
| epoch   2 |  1800/ 2928 batches | lr 4.75 | ms/batch 21.21 | loss  5.64 | ppl   281.60
| epoch   2 |  2000/ 2928 batches | lr 4.75 | ms/batch 21.23 | loss  5.66 | ppl   286.53
| epoch   2 |  2200/ 2928 batches | lr 4.75 | ms/batch 21.20 | loss  5.53 | ppl   253.34
| epoch   2 |  2400/ 2928 batches | lr 4.75 | ms/batch 21.22 | loss  5.64 | ppl   280.90
| epoch   2 |  2600/ 2928 batches | lr 4.75 | ms/batch 21.22 | loss  5.63 | ppl   280.05
| epoch   2 |  2800/ 2928 batches | lr 4.75 | ms/batch 21.22 | loss  5.57 | ppl   262.29
-----------------------------------------------------------------------------------------
| end of epoch   2 | time: 64.46s | valid loss  5.61 | valid ppl   272.03
-----------------------------------------------------------------------------------------
| epoch   3 |   200/ 2928 batches | lr 4.51 | ms/batch 21.33 | loss  5.59 | ppl   266.92
| epoch   3 |   400/ 2928 batches | lr 4.51 | ms/batch 21.26 | loss  5.61 | ppl   272.59
| epoch   3 |   600/ 2928 batches | lr 4.51 | ms/batch 21.25 | loss  5.40 | ppl   221.98
| epoch   3 |   800/ 2928 batches | lr 4.51 | ms/batch 21.21 | loss  5.47 | ppl   236.72
| epoch   3 |  1000/ 2928 batches | lr 4.51 | ms/batch 21.20 | loss  5.42 | ppl   226.42
| epoch   3 |  1200/ 2928 batches | lr 4.51 | ms/batch 21.21 | loss  5.46 | ppl   235.14
| epoch   3 |  1400/ 2928 batches | lr 4.51 | ms/batch 21.19 | loss  5.48 | ppl   240.08
| epoch   3 |  1600/ 2928 batches | lr 4.51 | ms/batch 21.22 | loss  5.51 | ppl   247.20
| epoch   3 |  1800/ 2928 batches | lr 4.51 | ms/batch 21.21 | loss  5.46 | ppl   234.06
| epoch   3 |  2000/ 2928 batches | lr 4.51 | ms/batch 21.20 | loss  5.47 | ppl   237.55
| epoch   3 |  2200/ 2928 batches | lr 4.51 | ms/batch 21.20 | loss  5.34 | ppl   208.68
| epoch   3 |  2400/ 2928 batches | lr 4.51 | ms/batch 21.20 | loss  5.45 | ppl   232.34
| epoch   3 |  2600/ 2928 batches | lr 4.51 | ms/batch 21.20 | loss  5.45 | ppl   233.68
| epoch   3 |  2800/ 2928 batches | lr 4.51 | ms/batch 21.19 | loss  5.39 | ppl   220.15
-----------------------------------------------------------------------------------------
| end of epoch   3 | time: 64.44s | valid loss  5.55 | valid ppl   258.24
-----------------------------------------------------------------------------------------

Evaluate the best model on the test dataset

test_loss = evaluate(best_model, test_data)
test_ppl = math.exp(test_loss)
print('=' * 89)
print(f'| End of training | test loss {test_loss:5.2f} | '
      f'test ppl {test_ppl:8.2f}')
print('=' * 89)

Out:

=========================================================================================
| End of training | test loss  5.46 | test ppl   236.20
=========================================================================================